2020
Теория динамических систем и бифуркаций
Название: Locking and regularization of chimeras by periodic forcing
Авторы: Bolotov M. I., Smirnov L. A., Osipov G. V., Pikovsky.
Журнал: PHYSICAL REVIEW E
Описание:
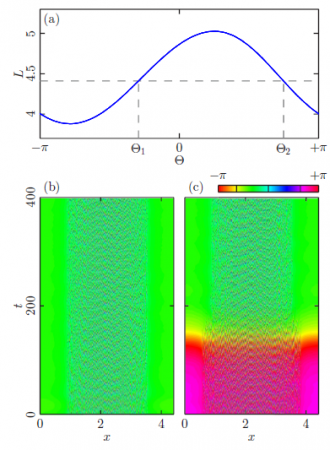
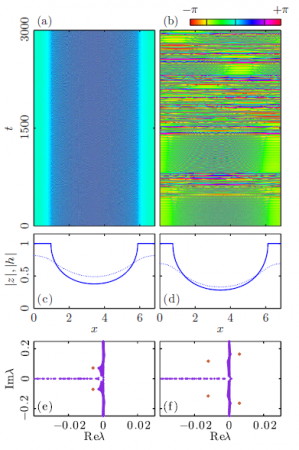
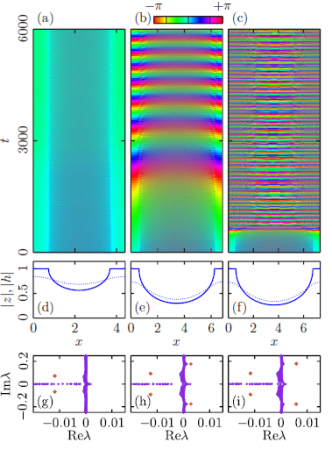
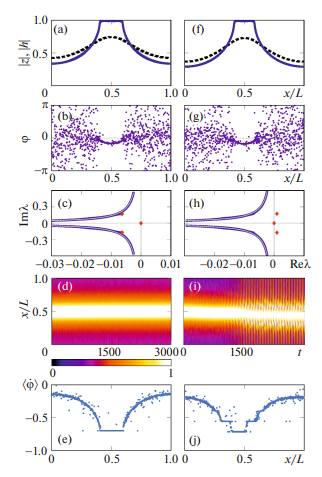
Исследованы явления синхронизации и регуляризации стационарных химерных состояний в среде идентичных не локально связанных фазовых осцилляторов с экспоненциально спадающим ядром, определяющим связь, находящейся под воздействием внешнего периодического сигнала.
Для рассматриваемой системы фазовых осцилляторов на основании редукции Отта-Антонсена были получены динамические уравнения относительно мезоскопических полей, определяющих степень синхронности элементов по фазе в окрестности каждой точки среды. Химерные режимы найдены как периодические траектории в фазовом пространстве вспомогательной системы обыкновенных дифференци-альных уравнений четвертого порядка.
Разработан метод построения области захвата (языка Арнольда) для стационарных химер. Показано, что внешний периодический сигнал, действующий на устойчивую химеру, приводит к захвату частоты когерентного кластера и увеличению его размера. Также показано, что за счет внешнего сигнала достаточной амплитуды можно добиться регуляризации бризерного и турбулентного химерных режимов.
Название: Пространственно-временные режимы в системе неидентичных осцилляторов Курамото-Баттогтоха
Авторы: Болотов М. И., Смирнов Л. А., Бубнова Е. С., Осипов Г. В., Пиковский А. С.
Журнал: Журнал экспериментальной и теоретической физики. 159(1), стр. 150-175 (2021)
Описание:
Рассмотрен ансамбль, состоящий из большого числа не локально связанных неидентичных фазовых осцилляторов, которые равномерно распределены на отрезке с периодическим граничными условиями.
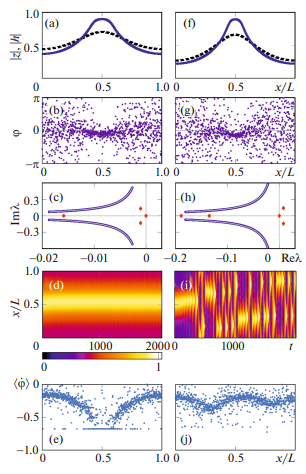
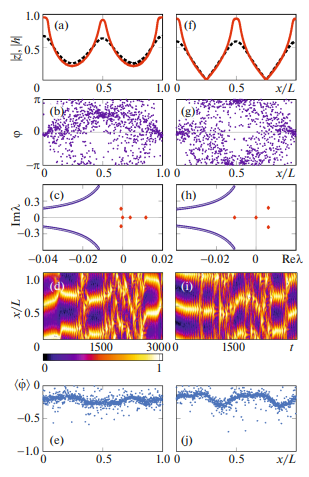
При этом предполагалось, что собственные частоты задаются независимо случайным образом согласно распределению Лоренца, а взаимодействие между осцилляторами ослабевает по экспоненциальному закону. C использованием процедуры усреднения было получено динамическое уравнение Отта–Антонсена для локального комплексного параметра порядка, характеризующего степень фазовой скоррелированности элементов в малой окрестности произвольной точки рассматриваемой осцилляторной среды. В рамках этого уравнения, прежде всего, были найдены стационарные (равномерно вращающиеся) режимы с постоянным по модулю значением локального параметра порядка. Установлено, что среди таких состояний можно выделить два вида: однородные и градиентные.
Далее, была определена их устойчивость с помощью анализа спектра собственных значений соответствующих линеаризованных уравнений. Показано, что при больших значениях полуширины функции распределения собственных частот реализуется только полностью асинхронный режим с нулевым средним полем. Если же полуширина случайного разброса становится меньше некоторой пороговой величины, то данное состояние перестает быть устойчивым, а в системе могут наблюдаться как однородные, так и градиентные частично синхронные режимы в зависимости от размеров среды и фазового сдвига. Воспользовавшись тем, что взаимодействие между элементами убывает экспоненциальным образом, интегро-дифференциальное уравнение Отта–Антонсена было преобразовано к само-согласованной системе уравнений в частных производных. Это позволило предложить метод эффективного поиска стационарных (равномерно вращающихся) неоднородных пространственных структур, которые в пределе одинаковых элементов переходят в химерные состояния. Основная идея данного метода состоит в построении замкнутых траекторий в фазовом пространстве вспомогательной системы обыкновенных дифференциальных уравнений третьего порядка. Отметим, что подобным периодическим решениям несложно поставить в соответствие неподвижные точки двумерного отображения. После того, как были найдены примеры неоднородных профилей локального комплексного параметра порядка и по ним восстановлены распределения фаз, анализировалась устойчивость полученных состояний как с помощью расчета спектра линейных возмущений, так и с использованием прямого численного моделирования. Для проведения такого рода анализа потребовалось, в частности, разработать и адаптировать процедуру расчета непрерывной и дискретной составляющих спектра собственных значений линеаризованного вокруг одного из стационарных образований интегро-дифференциальное уравнение Отта –Антонсена.
В итоге, установлено, что среди неоднородных состояний со статичным рас-пределением областей с повышенной и пониженной степенью синхронизации устойчивыми (в строгом смысле) являются только те режимы, для которых у профиля локального параметра порядка имеет только один максимум. Однако среди остальных найденных нами структур встречаются слабо неустойчивые (транзиентные) образования. С помощью прямого численного моделирования в рамках исходной системы удалось подтвердить данные выводы и показать, что обсуждаемые квазихимерные режимы (как предельные, так и транзиентные) вращения играют важную роль в динамике ансамбля из большого числа неиндентичных не локально связанных фазовых осцилляторов с экспоненциальным типом взаимодействия, так как одни из них устанавливаются и в последствии не разрушаются, а другие возникают в виде переходных продолжительных процессов между интервалами со сложным нерегулярным поведением усредненных полей.
Заложены основы теории смешанной динамики, нового явления, связанного с возможностью пересечения аттракторов и репеллеров, и построены базовые примеры. Разработаны методы построения обратимых аналитических возмущений сохраняющих площадь отображений, изучены бифуркации потери симметрии в обратимых отображениях Эно и их композициях (двойных отображениях Эно).
Построен пример дикого спирального аттрактора четырехмерной системы диф-ференциальных уравнений, исследованы его топологические и геометрические свойства, созданы новые математические методы проверки гиперболических и псевдогиперболических свойств странных аттракторов. Построена качественная теория дискретных аттракторов Лоренца, найдены их примеры в трехмерных отображениях Эно.
Исследованы бифуркации, приводящие к возникновению гиперхаотических аттра-кторов в четырехмерной системе Ресслера. Открыто и численно исследовано явление «скачка гиперхаотичности», связанное с кризисами «скрытых» аттракторов.
Изучены солитоны и кавитоны (локализованные решения с особенностями) не-локального интегро-дифференциального уравнения Уизема. Построены различные типы локализованных решений как с монотонной, так и с осциллирующей асимптотикой.
Построены основные элементы качественной теории транзиторных неконсерва-тивных систем, исследован ряд таких систем из приложений. Исследованы динамика и бифуркации резонансов в квазипериодических возмущениях двумерных нели-нейных гамильтоновых систем.
Математическое моделирование и исследование нелинейной динамики систем и процессов управления
Название: Dynamics of spiking map-based neural networks in problems of supervised learning
Авторы: Mechislav M. Pugavko, Oleg V. Maslennikov, Vladimir I. Nekorkin.
Журнал: Communications in Nonlinear Science and Numerical Simulation 90(4):105399
Описание:
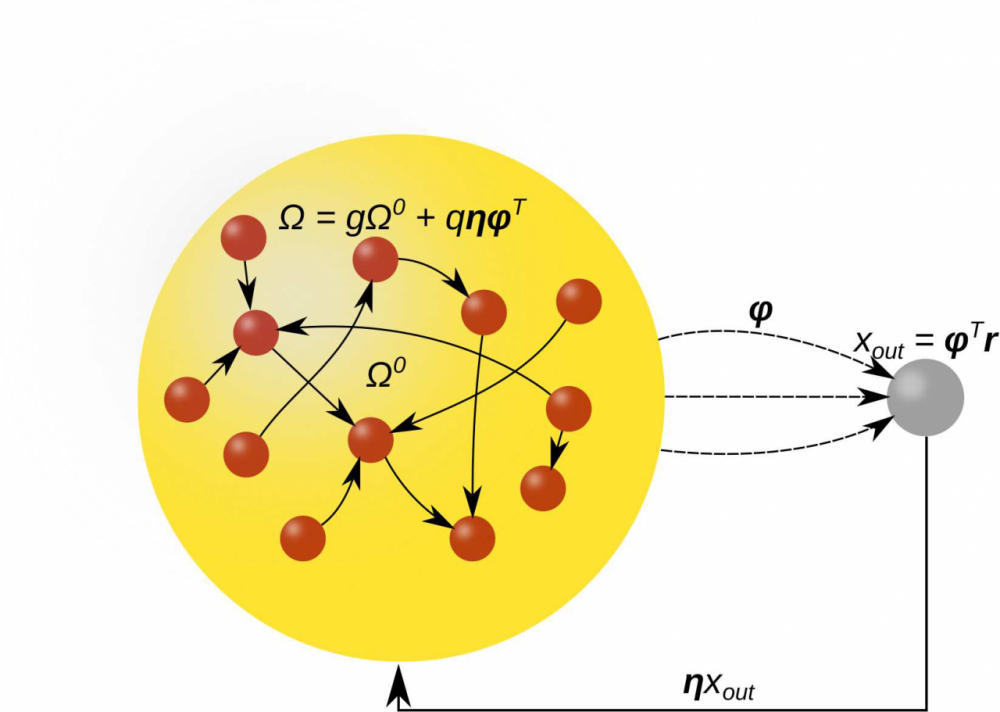
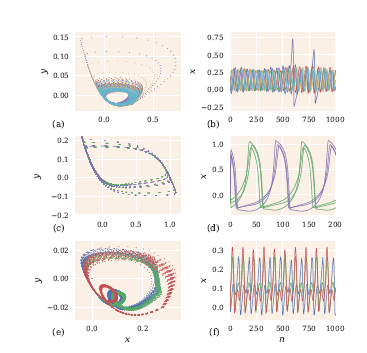
Предложена и исследована система резервуарных вычислений, которая обучается автономно воспроизводить периодический целевой сигнал после обучения. Резервуар состоит из сети дискретных моделей нейронов (Курбажа-Некоркина) с обратной связью между выходом и сетью нейронов. Обучение системы осуществляется с помощью метода обучения FORCE. Рассмотрены два случая. В первом случае все нейроны в сети идентичны. Была проанализирована ошибка в плоскости параметров частоты целей функции и параметра, отвечающего за частоту генерации спайков нейронами. Во втором случае изучалась неоднородная сеть, неоднородность которой задавалась с помощью разброса параметра, который отвечает за частоту генерации спайков. Обнаружено, что неоднородность может увеличивать диапазон частот целевой периодической функции, которые может воспроизводить система резервуарных вычислений после обучения. Также мы проанализировали влияние параметров связей на качество обучения. Исследована пространственно-временная динамика с помощью исследования пространственно-временных диаграмм, динамики отдельных нейронов в сети и траектории в пространстве первых трех главных компонент. Установлены механизмы, которые приводят к правильному воспроизведению периодического выхода после обучения. В процессе обучения траектория изменяется. До обучения система демонстрирует хаотическое поведение, а после обучения в фазовом пространстве всей системы существует устойчивая периодическая траектория, соответствующая периоди-ческому выходу.
Название: Циклы-утки и торы-утки в слабо неоднородном ансамбле нейронов ФитцХью-Нагумо с возбуждающими связями
Авторы: А. А. Макеева, А. С. Дмитричев, В. И. Некоркин.
Журнал: Известия вузов. ПНД. 2020
Описание:
Изучена динамика слабо-неоднородного ансамбля из трех нейронов Фитц-Хью-Нагумо, уровни деполяризации которых линейно растут с их индексом, и со-единенных последовательно посредством химических синапсов. Предполагается, что в отсутствии связей нейроны находятся в состоянии покоя. Первый нейрон при этом всегда остается в состоянии покоя, но может возбудить колебания во втором нейроне, а тот, в свою очередь, может возбудить колебания в третьем. При это из-за наличия положительной неоднородности сначала возбуждаются колебания в третьем нейроне, а уже после – во втором. Таким образом коллективная динамика ансамбля формируется воздействием колебаний второго нейрона на возбужденные им же колебания в третьем нейроне. Динамика второго нейрона была изучена аналитически.
Показано существование в соответствующей системе решений, отвечающих различным типам периодических, в том числе уточных, колебаний. С помощью приближенной системы в соответствующей третьему нейрону системе предсказано существование, в том числе уточных, торов. Построено разбиение плоскости параметров на области с различным поведением нейронов ансамбля. Показано, что при малых силах межнейронных связей в ансамбле, независимо от уровня деполяризации нейронов, наблюдаются различные режимы подпороговых колебаний, прообразом которых являются торы и резонансные циклы, в том числе уточного типа. При больших силах связей наблюдаются два режима спайковых колебаний, в которых второй нейрон ансамбля демонстрирует периодические колебания, а третий либо периодические, либо квазипериодические колебания. При промежуточных силах связей можно получить в ансамбле как подпороговые, так и спайковые колебания. Установлено, что переход от подпороговых колебаний к спайковым происходит через области, отвечающие установлению в ансамбле режимов амплитудно-модулированных подпороговых, амплитудно-модулированных спайковых и смешанных подпорогово-спайковых колебаний. Эти области отвечают существованию в фазовом пространстве соответствующей динамической системы сложных “уточных торов”.
Название: Метод определения характеристик перемежающейся обобщенной синхронизации на основе расчета локальных показателей Ляпунова
Авторы: Москаленко О. И., Евстифеев Е. В., Короновский А. А.
Журнал: Письма в ЖТФ. 46, 16 (2020) 12-15
Англоязычная версия :
Название: Intermittent route to generalized synchronization in bidirectionally coupled chaotic oscillators
Авторы: Koronovskii A. A., Moskalenko O. I., Pivovarov A. A., Evstifeev E. V.
Журнал: CHAOS. 30, 8 (2020) 083133
Описание:
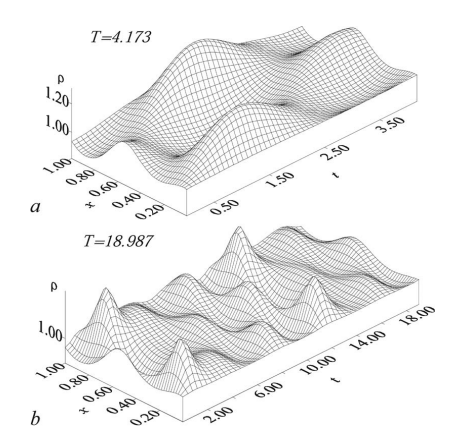
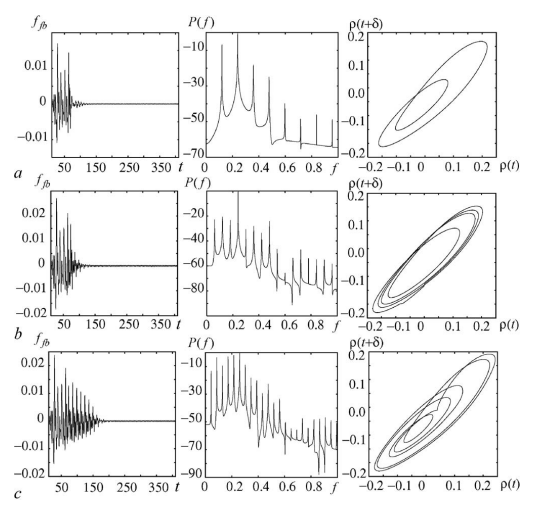
Предложен метод нахождения и анализа характерных участков временных реа-лизаций сложных нелинейных систем, находящихся во взаимодействии друг с другом, в случае сосуществования в динамике систем нескольких характерных режимов, последовательно сменяющих друг друга. Данный подход основан на расчете спектра ограниченных во времени показателей Ляпунова по известному оператору эволюции. Метод применен как для различных типов взаимодействия между системами, так и для различных рассматриваемых систем. В случаях, допускающих сопоставление полученных результатов с результатами, полученными с помощью других подходов, их сравнение дает хорошее соответствие. Получены статистические характеристики поведения анализируемых динамических систем, находящихся в рассматриваемых режимах
Название: Метод выделения характерных фаз поведения в системах со сложной топологией аттрактора, находящихся вблизи границы обобщенной синхронизации
Авторы: Москаленко О. И., Короновский А. А., Ханадеев В. А.
Журнал: Изв. Вузов. Прикладная нелинейная динамика. 28, 3 (2020) 274-281
Англоязычная версия :
Название: Jump intermittency as a second type of transition to and from generalized synchronization
Авторы: Koronovskii A. A., Moskalenko O. I., Pivovarov A. A., Khanadeev V. A., Hramov A. E., Pisarchik A. N.
Журнал: Phys. Rev. E. 102, (2020) 012205
Описание:
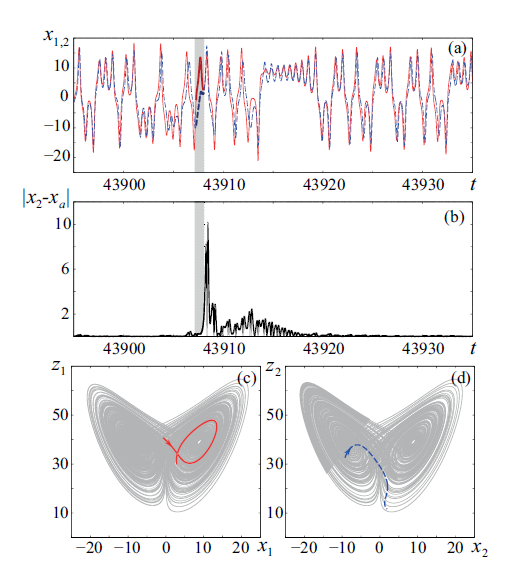
Предложен метод нахождения и анализа характерных участков временных реа-лизаций взаимодействующих друг с другом нелинейных систем, характеризующихся сложной геометрической топологией хаотического аттрактора в фазовом прос-транстве, при которой аттрактор состоит из нескольких различающихся подмножеств. При определенном наборе значений управляющих параметров в поведении изучаемых систем могут сосуществовать нескольких характерных динамических режимов, отличающихся количественно и качественно, которые последовательно сменяют друг друга с течением времени. Метод основан на анализе изменения расположения изображающих точек в фазовом пространстве взаимо-действующих систем с учетом расположения характерных подмножеств, образующих фазовые портреты изучаемых осцилляторов. Работоспособность метода проверена для различных модельных систем и различных видов взаимодействия между ними, получены статистические характеристики, описывающие сосуществование динамику последовательно сменяющих друг друга с течением времени динамических режимов.
Название: Extended detrended fluctuation analysis of sound-induced changes in brain electrical activity
Авторы: Pavlov A. N., Dubrovsky A. I., Koronovskii A. A. Jr., Pavlova O. N., Semyachkina Glushkovskaya O. V., Kurths J.
Журнал: Chaos, Solitons & Fractals 139, (2020) 109989
Название: Extended detrended fluctuation analysis of electroencephalograms signals during sleep and the opening of the blood–brain barrier
Авторы: Pavlov A. N., Dubrovsky A. I., Koronovskii A. A. Jr., Pavlova O. N., Semyachkina Glushkovskaya O.V., Kurths J.
Журнал: Chaos 30, (2020) 073138
Описание:
Проведена модификация метода флуктуационного анализа нестационарных процес-сов, применяющего процедуру вычисления профиля сигнала, его сегментирование, кусочно-линейную аппроксимацию для моделирования медленных изменений среднего уровня (тренда) и расчет среднеквадратичных отклонений профиля от выбранной модели тренда. Предложенная модификация включает дополнительный анализ степенной зависимости вариаций локальных среднеквадратичных откло-нений от размера сегмента для количественного описания эффектов неста-ционарности в экспериментальных данных. Проведено исследование влияния разных типов нестационарности, включая медленные вариации среднего уровня, сосуществование нескольких характерных режимов, изменения во времени дисперсии анализируемого процесса. Наряду с тестированием модифицированного метода на различных примерах сигналов с известными статистическими характеристиками, рассмотрено его применение для диагностики состояния физиологических систем по экспериментальным данным.
Название: Ellipsoidal reachable sets of linear time-varying continuous and discrete systems in control and estimation problems
Авторы: Balandin D. V., Biryukov R. S., Kogan M. M.
Журнал: Automatica.116(6). 108926 (2020)
Название: Control and estimation in linear time-varying systems based on ellipsoidal reachability sets
Авторы: Balandin D. V., Kogan M. M.
Журнал: Automation and Remote Control.81(8). 1367–1384 (2020)
Описание:
Показано, что множеством достижимости линейной нестационарной непрерывной или дискретной системы, в которой сумма квадратичной формы начального состояния и интеграла или суммы квадратичных форм возмущения на конечном интервале времени ограничена сверху заданной величиной, является эволюционирующий эллипсоид. Матрица эллипсоида удовлетворяет линейному матричному дифференциальному или разностному уравнению соответственно. Синтезированы оптимальные эллипсоидальные наблюдатель и алгоритм иден-тификации, обеспечивающие наилучшие эллипсоидальные оценки состояния системы и неизвестных параметров, а также оптимальные регуляторы, обеспечивающие попадание состояния системы в целевое множество или удержание траектории системы в эллипсоидальной трубке. Установлено соответствие между оптимальным эллипсоидальным наблюдателем и фильтром Калмана. Приведены иллюстрирующие примеры для уравнения Матье, описывающего параметрические колебания линейного осциллятора. На рисунке представлена эволюция во времени эллипсоидальных оценок состояния динамической системы.
В рамках однодоменной модели Ландау-Лифшица с дополнительным слагаемым Слончевского-Берже исследовано асимметричное относительно инверсии магнитных моментов влияние поляризации ферромагнитных слоев на динамические и статистические характеристики колебаний спин-трансферного нано осциллятора. Для актуального, с точки зрения практических приложений, случая малых значений коэффициента, отражающего асимметричное влияние спинового тока в слагаемом Слончевского-Берже, было получено аналитическое выражение зависимости средней частоты спинового генератора от данного коэффициента асимметрии, интенсивности шума магнитного поля, плотности спин-поляризованного тока и величины детерминированной составляющей внешнего магнитного поля в статистически аксиально-симметричном случае. Показано, что рост интенсивности шума приводит, с одной стороны – к увеличению шумоиндуцированного сдвига средней частоты генерации, но с другой – к частичной компенсации асимметричного отклонения зависимостей средних частот генерации от соответствующих зависимостей при отсутствии асимметрии.
Исследование динамики больших ансамблей нейронов мозга – одна из наиболее трудных, интересных и актуальных проблем современной науки, привлекающая внимание ученых, как в теоретическом плане, так и в области эксперимента. Важным аспектом изучения остаются особенности синхронизации активности нейронов. Исследована синхронизации пачечных колебаний нейронов. Изучена динамика двух взаимодействующих нейроподобных генераторов на основе системы фазовой автоподстройки частоты с полосовым фильтром. Поскольку подобная система может быть реализована в виде электронного устройства, то исследование проводилось при помощи среды системотехнического моделирования Simulink. Рассмотрена динамика пары нейроподобных генераторов, связанных однонаправленной импульсной связью, имитирующей синаптическое воздействие. Найдены области синхронизации для нейронов с различным типом пачечной активности и изучены особенности синхронизации в зависимости от параметров взаимодействия, в частности, фазовые соотношения в синхронном режиме.
Разработана модель формирования пачечных разрядов в нейрон-глиальной сети. В модели было показано, что астроциты способны осуществлять двунаправленную регуляцию нейронной активности. Нейрон-астроцитарное взаимодействие приводит к формированию пачечной нейрональной активности. Более того, бистабильный режим астроцитарной активности может приводить к спонтанным переходам между состояниями нейронной сети.
С использованием метода Кольского и его модификаций проведены экспериментальные исследования деформирования и разрушения образцов липы и сосны. Испытания образцов, вырезанных вдоль и поперек волокон, показали сильную анизотропию свойств и их скоростных зависимостей. Результаты испытаний использовались для идентификации математической модели, описывающей поведение древесины (MAT_WOOD из ПП LS-DYNA). Проведена верификация модели на базе эксперимента на динамическое внедрение полусферического индентора в образцы из древесины. Полученная информация может быть использована для проведения достоверного численного анализа проектируемых конструкций контейнеров для транспортирования опасных веществ, использующих в своем составе в качестве компонентов, демпфирующих ударные нагрузки, древесину.
В мазере на циклотронном резонансе миллиметрового диапазона экспериментально наблюдалось гиперхаотическая динамика, при которой существенно положите-льными являются два показателя Ляпунова. При этом расчетная размерность аттракторов достигает значений 4, а фазовый портрет приобретает вид фрактального объемного множества, что может быть объяснено взаимодействием пучка с большим количеством продольных мод в длинной системе. Показано, что аналогичное поведение характерно и для модели винтовой гиро-ЛБВ с запаздывающей обратной связью, где число существенно положительных показателей Ляпунова может достигать 4.Показано существование устойчивых солитоноподобных решений в условиях циклотронно-резонансного взаимодействия микроволнового излучения с прямолинейным электронным потоком. Найдены частные случаи, при которых полученное решение сводится к форме, аналогичной для процессов формирования солитонов самоиндуцированной прозрачности при распространении оптического импульса через пассивную двухуровневую среду. Для выполнения оптимизации параметров мощных гиротроновтерагерцового диапазона разработан комплекс программ с современным графическим интерфейсом, включающий моделирование в рамках стационарной задачи, сводящейся к задаче Штурма–Лиувилля для уравнения неоднородной струны, и нестационарной, совмещающей уравнение Шредингера и систему уравнений движения электронов. На основе разработанных программ выполнены расчеты гиротрона диапазона 500 ГГц.
Методы высокопроизводительных вычислений для научных и прикладных исследований мирового уровня
Задачи многокритериальной оптимизации (MCO) относятся к числу наиболее сложных постановок задач принятия решений и широко встречаются в приложениях. Ключевой особенностью задач MCO является отсутствие в большинстве случаев единственного решения, которое было бы наилучшим сразу по всем критериям эффективности в силу их возможной противоречивости. При этом в прикладных задачах критерии эффективности могут иметь сложный многоэкстремальный вид, а область допустимых вариантов может определяться невыпуклыми ограничениями. Среди известных подходов к решению задач указанного класса можно выделить методы лексикографической оптимизации, когда осуществляется то или иное упорядочивание критериев по важности и оптимизация осуществляется в порядке их упорядоченности (MCOlex).
В рамках проведенного исследования был разработан новый подход к решению задач MCOlex, который основывается на следующих основных положениях:
– Решение задачи сводится к решению последовательности задач глобальной оп-тимизации с невыпуклыми ограничениями (GO);
– Для решения задач GO применяются эффективные алгоритмы глобального поиска, разработанные в рамках информационно-статистической теории многоэкстре-мальной оптимизации;
– При выполнении всех необходимых вычислений полностью используется вся поисковая информация, получаемая в процессе решения задачи MCOlex.
Разработанный подход позволяет существенно уменьшить объем выполняемых вычислений вплоть до выполнения всего лишь нескольких итераций при поиске очередных эффективных решений. Результаты проведенного исследования отражены в статье в журнале Optimization Letters (Q2). Отметим, что методы решения задач многокритериальной многоэкстремальной оптимизации, раз-виваемые в данном исследовании, основаны на идее редукции исходной многомерной задачи к эквивалентной одномерной или к системе одномерных подзадач с последующим решением одномерных задач эффективными методами оптимизации функций одной переменной. Известно две такие схемы: редукция на основе кривых, заполняющих пространство (кривых Пеано, или разверток) и схема рекурсивной вложенной оптимизации (многошаговая схема). При выполнении исследований в 2020 году была предложена обобщенная схема редукции размерности, комбинирующая использование вложенной оптимизации и кривых Пеано. При таком подходе вложенные подзадачи могут быть как одномерными, так и многомерными; в последнем случае для редукции размерности вложенных подзадач используются развертки. Результаты проведенного исследования отражены в статье, опубликованной в журнале Automation and Remote Control, Scopus (Q2).
Название: Transforming Lindblad Equations into Systems of Real-Valued Linear Equations: Performance Optimization and Parallelization of an Algorithm
Авторы: Meyerov, I., Kozinov, E., Liniov, A., Volokitin, V., Yusipov, I., Ivanchenko, M., Denisov, S.
Журнал: Entropy2020, 22, 1133. (Q2)
Описание:
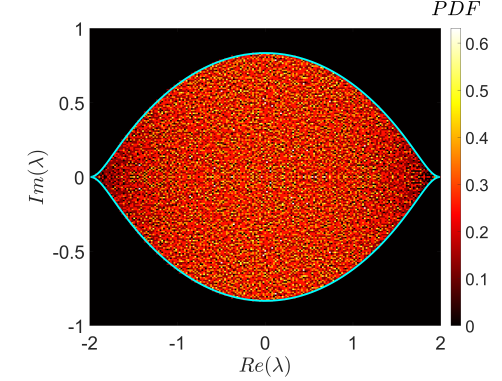
Значительный прогресс был достигнут в направлении высокопроизводительных алгоритмов для исследования открытых квантовых систем и моделирования их динамки. Нами были достигнуты новые «рекордные показатели» в смысле размерности исследуемых моделей. Были исследованы перспективные методы числовых квантовых симуляций (digital quantum simulations), которые могут быть применены для симуляции открытых квантовых систем на квантовых компьютерах кубитной архитектуры. В области динамики сложных классических систем, нами были разработаны и программно реализованы алгоритмы для симуляции динамики сложных сетей (networks) и плазмы. Группа разработала и оптимизировала пакет программных средств для реализации программы вычислительных экспериментов. Несколько серий таких экспериментов были проведены с использованием возможностей современных параллельных вычислительных систем.
Методы и модели искусственного интеллекта
Исследуется проблема репрезентации в сверточных нейронных сетях. Разобраны причины того, что на определенных типах данных сверточный блок строит не интерпретируемую репрезентацию. Предложен концептуальный подход к устранению проблемы: приведены обоснования того, что использование графов для промежуточной репрезентации может “починить” семантическую арифметику в пространстве кодов. Приведено обоснование предложенного подхода с точки зрения биологического правдоподобия при моделировании интеллекта.
Название: LUDB: New Open-Access Validation Tool for Electrocardiogram Delineation Algorithms
Авторы: Kalyakulina A. I., Yusipov I. I., Moskalenko V. A., Nikolyskii A. V., Kosonogov K. A., Osipov G. V., Zolotykh N. Yu., Ivanchenko M. V.
Журнал: IEEE Access. 2020. No. 8. P. 9214911
Описание:
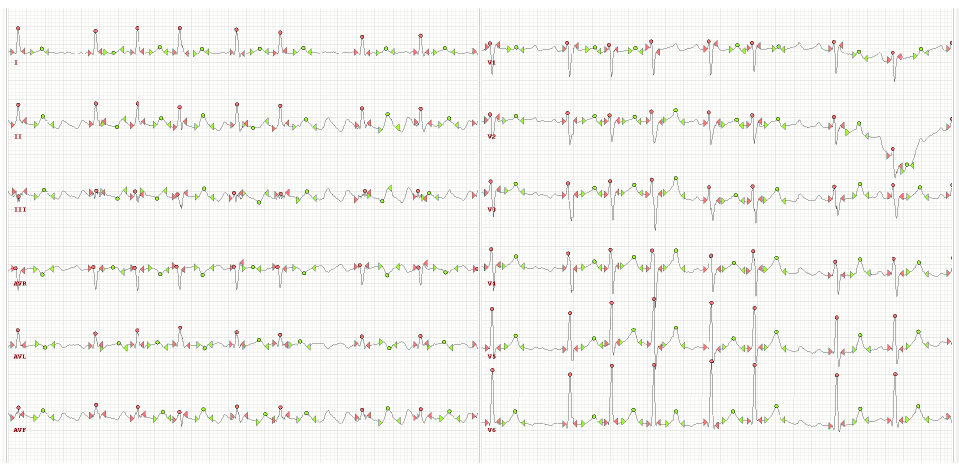
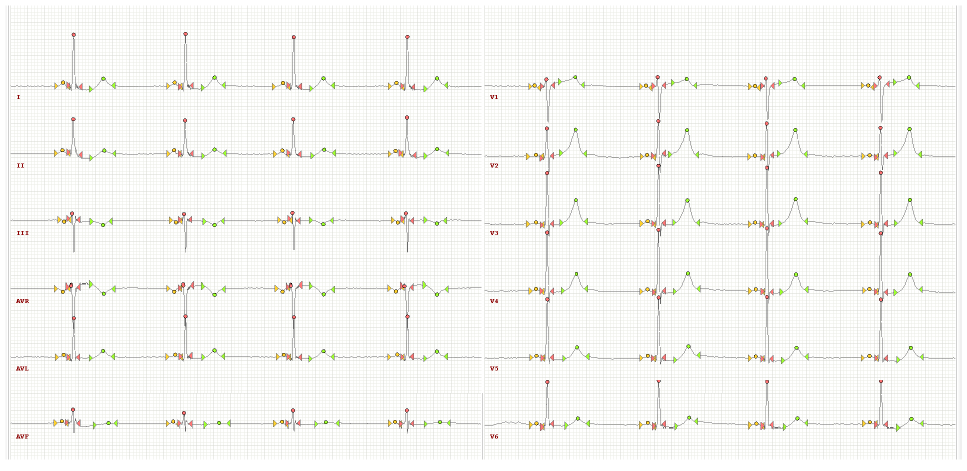
Собрана и описана базе данных ЭКГ-сигналов Lobachevsky University Database (LUDB), представляющая собой открытый инструмент для проверки алгоритмов опре-деления границ ЭКГ, который превосходит существующие общедоступные базы данных по нескольким аспектам. LUDB содержит 200 записей 10-секундных электрокардиограмм (ЭКГ) в 12 отведениях от разных субъектов, представляющих различные морфологии сигналов. Границы и пики комплексов QRS и зубцов P и T размечены вручную кардиологами. На данной базе продемонстрировано преимущество алгоритмов автоматической сегментации ЭКГ, разработанных авторским коллективом.
Рассматриваются 2-пороговые функции, заданные на двумерной целочисленной решетке размера m x n, то есть функции, представляемые как конъюнкция двух пороговых функций. Предлагается характеризация 2-пороговых функций выпуклыми парами направленных простых отрезков. Указанная характеризация впоследствии может использоваться для подсчета количества 2-пороговых функций. Впервые получена асимптотическая формула числа 2-пороговых функций, зависящая от параметров m и n. Интерес к пороговым функциям и их модификациям в настоящее время вызван в первую очередь потребностями машинного обучения и искус-ственного интеллекта.
